scipy.stats.

常態#

class scipy.stats.Normal(mu=None, sigma=None, **kwargs)[source]#

具有指定平均值和標準差的常態分佈。

常態分佈的機率密度函數為

\[f(x) = \frac{1}{\sigma \sqrt{2 \pi}} \exp { \left( -\frac{1}{2}\left( \frac{x - \mu}{\sigma} \right)^2 \right)}\]

對於 \(x\) 屬於 (-infty, infty)。此類別接受一種參數化：mu 對應 \(\mu \in (-\infty, \infty)\)，sigma 對應 \(\sigma \in (0, \infty)\)。

參數:

tol正浮點數，選填: 計算所需的相對容忍度。若未指定，計算速度可能會更快；若提供，計算結果可能更符合所需的準確度。
validation_policy{None, “skip_all”}: 指定要執行的輸入驗證級別。若未指定，則會執行輸入驗證，以確保在邊緣情況（例如參數超出範圍、引數超出分佈支援等）下的適當行為，並提高輸出 dtype、形狀等的一致性。傳遞 'skip_all' 以避免在可接受粗糙邊緣時，進行這些檢查的計算開銷。
cache_policy{None, “no_cache”}: 指定快取中間結果的程度。若未指定，則會快取某些計算的中間結果（例如分佈支援、動差等），以提高未來計算的效能。傳遞 'no_cache' 以減少類別實例保留的記憶體。

另請參閱

隨機變數轉換指南: 教學

註解

以下縮寫在整個文件中使用。

PDF：機率密度函數
CDF：累積分布函數
CCDF：互補累積分布函數
entropy：微分熵
log-F：F 的對數 (例如 log-CDF)
inverse F：F 的反函數 (例如 inverse CDF)

API 文件旨在描述 API，而非作為統計參考。我們力求在使用功能所需的層面上保持正確，而不是在數學上嚴謹。例如，連續性和可微分性可能會被隱含地假設。對於精確的數學定義，請查閱您偏好的數學文本。

範例

若要使用分佈類別，必須使用與其中一種接受的參數化相對應的關鍵字參數來實例化它。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> from scipy.stats import Normal
>>> X = Normal(mu=-0.81, sigma=0.69)

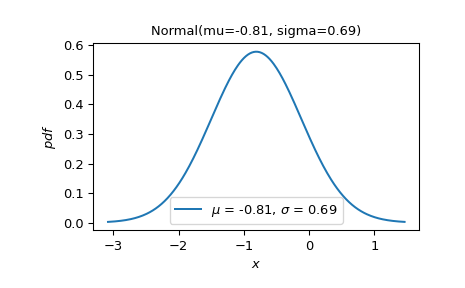
為了方便起見，可以使用 plot 方法來視覺化分佈的密度和其他函數。

>>> X.plot()
>>> plt.show()

../../_images/scipy-stats-Normal-1_00_00.png

可以使用 support 方法來取得底層分佈的支援。

>>> X.support()
(-inf, inf)

與所有參數化相關聯的參數數值可作為屬性使用。

>>> X.mu, X.sigma
(-0.81, 0.69)

若要在引數 x=-1.13 處評估底層分佈的機率密度函數

>>> x = -1.13
>>> X.pdf(x)
0.5192263911374636

累積分布函數、其互補函數以及這些函數的對數也以類似方式評估。

>>> np.allclose(np.exp(X.logccdf(x)), 1 - X.cdf(x))
True

這些函數對於引數 x 的反函數也可用。

>>> logp = np.log(1 - X.ccdf(x))
>>> np.allclose(X.ilogcdf(logp), x)
True

請注意，分佈函數及其對數也具有雙引數版本，可用於處理兩個引數之間的機率質量。結果往往比樸素的實作更準確，因為它避免了減法抵消。

>>> y = -0.56
>>> np.allclose(X.ccdf(x, y), 1 - (X.cdf(y) - X.cdf(x)))
True

有方法可以計算集中趨勢、離散程度、更高階動差和熵的度量。

>>> X.mean(), X.median(), X.mode()
(-0.81, -0.81, -0.81)
>>> X.variance(), X.standard_deviation()
(0.4760999999999999, 0.69)
>>> X.skewness(), X.kurtosis()
(0.0, 3.0)
>>> np.allclose(X.moment(order=6, kind='standardized'),
...             X.moment(order=6, kind='central') / X.variance()**3)
True
>>> np.allclose(np.exp(X.logentropy()), X.entropy())
True

可以使用 sample 從底層分佈中繪製偽隨機樣本。

>>> X.sample(shape=(4,))
array([ 0.16207254, -1.20075226, -0.88259226, -1.68711988])  # may vary

屬性:

所有參數都可作為屬性使用。

方法

`support`()	隨機變數的支援
`plot`([x, y, t, ax])	繪製分佈的函數。
`sample`([shape, method, rng])	從分佈中取得隨機樣本。
`moment`([order, kind, method])	正整數階的原始動差、中心動差或標準動差。
`mean`(*[, method])	平均值 (關於原點的原始一階動差)
`median`(*[, method])	中位數 (第 50 百分位數)
`mode`(*[, method])	眾數 (最可能的值)
`variance`(*[, method])	變異數 (中心二階動差)
`standard_deviation`(*[, method])	標準差 (中心二階動差的平方根)
`skewness`(*[, method])	偏度 (標準化三階動差)
`kurtosis`(*[, method, convention])	峰度 (標準化四階動差)
`pdf`(x, /, *[, method])	機率密度函數
`logpdf`(x, /, *[, method])	機率密度函數的對數
`cdf`(x[, y, method])	累積分布函數
`icdf`(p, /, *[, method])	累積分布函數的反函數。
`ccdf`(x[, y, method])	互補累積分布函數
`iccdf`(p, /, *[, method])	互補累積分布函數的反函數。
`logcdf`(x[, y, method])	累積分布函數的對數
`ilogcdf`(logp, /, *[, method])	累積分布函數對數的反函數。
`logccdf`(x[, y, method])	互補累積分布函數的對數
`ilogccdf`(logp, /, *[, method])	互補累積分布函數對數的反函數。
`entropy`(*[, method])	微分熵
`logentropy`(*[, method])	微分熵的對數