scipy.stats.nchypergeom_wallenius#

scipy.stats.nchypergeom_wallenius = <scipy.stats._discrete_distns.nchypergeom_wallenius_gen object>[source]#

Wallenius 非中心超幾何離散隨機變數。

Wallenius 非中心超幾何分佈模型，描述從箱子中抽取兩種物體。 M 是物體總數， n 是 Type I 物體的數量，而 odds 是勝算比：當每種類型只有一個物體時，選擇 Type I 物體而不是 Type II 物體的機率。隨機變數表示如果我們從箱子中一次一個地抽取預先確定的 N 個物體，則抽取的 Type I 物體的數量。

作為 rv_discrete 類別的一個實例， nchypergeom_wallenius 物件繼承了它的一組通用方法（完整列表請參見下文），並使用此特定分佈的詳細資訊來完善它們。

參見

nchypergeom_fisher, hypergeom, nhypergeom

註解

令數學符號 \(N\), \(n\) 和 \(M\) 分別對應於參數 N 、 n 和 M （如上定義）。

機率質量函數定義為

\[p(x; N, n, M) = \binom{n}{x} \binom{M - n}{N-x} \int_0^1 \left(1-t^{\omega/D}\right)^x\left(1-t^{1/D}\right)^{N-x} dt\]

for \(x \in [x_l, x_u]\), \(M \in {\mathbb N}\), \(n \in [0, M]\), \(N \in [0, M]\), \(\omega > 0\), where \(x_l = \max(0, N - (M - n))\), \(x_u = \min(N, n)\),

\[D = \omega(n - x) + ((M - n)-(N-x)),\]

and the binomial coefficients are defined as

\[\binom{n}{k} \equiv \frac{n!}{k! (n - k)!}.\]

nchypergeom_wallenius 使用 Agner Fog 的 BiasedUrn 套件，並獲得許可在 SciPy 的許可證下發佈。

用於表示形狀參數（ N 、 n 和 M ）的符號並非普遍接受；選擇它們是為了與 hypergeom 一致。

請注意， Wallenius 非中心超幾何分佈與 Fisher 非中心超幾何分佈不同，後者模型描述一次從箱子中取出一把物體，然後才發現取出了 N 個物體。然而，當勝算比為 1 時，這兩種分佈都簡化為普通超幾何分佈。

上面的機率質量函數以「標準化」形式定義。若要移動分佈，請使用 loc 參數。具體來說， nchypergeom_wallenius.pmf(k, M, n, N, odds, loc) 與 nchypergeom_wallenius.pmf(k - loc, M, n, N, odds) 完全等效。

參考文獻

[1]

Agner Fog, “Biased Urn Theory”。 https://r-cran.dev.org.tw/web/packages/BiasedUrn/vignettes/UrnTheory.pdf

[2]

“Wallenius’ noncentral hypergeometric distribution”，維基百科， https://en.wikipedia.org/wiki/Wallenius’_noncentral_hypergeometric_distribution

範例

>>> import numpy as np
>>> from scipy.stats import nchypergeom_wallenius
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

計算前四個動差

>>> M, n, N, odds = 140, 80, 60, 0.5
>>> mean, var, skew, kurt = nchypergeom_wallenius.stats(M, n, N, odds, moments='mvsk')

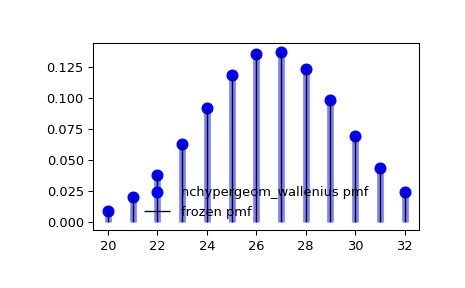
顯示機率質量函數 (pmf)

>>> x = np.arange(nchypergeom_wallenius.ppf(0.01, M, n, N, odds),
...               nchypergeom_wallenius.ppf(0.99, M, n, N, odds))
>>> ax.plot(x, nchypergeom_wallenius.pmf(x, M, n, N, odds), 'bo', ms=8, label='nchypergeom_wallenius pmf')
>>> ax.vlines(x, 0, nchypergeom_wallenius.pmf(x, M, n, N, odds), colors='b', lw=5, alpha=0.5)

或者，可以呼叫分佈物件（作為函數）來固定形狀和位置。這會傳回一個「凍結」的 RV 物件，其中包含給定的固定參數。

凍結分佈並顯示凍結的 pmf

>>> rv = nchypergeom_wallenius(M, n, N, odds)
>>> ax.vlines(x, 0, rv.pmf(x), colors='k', linestyles='-', lw=1,
...         label='frozen pmf')
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

../../_images/scipy-stats-nchypergeom_wallenius-1_00_00.png

檢查 cdf 和 ppf 的準確性

>>> prob = nchypergeom_wallenius.cdf(x, M, n, N, odds)
>>> np.allclose(x, nchypergeom_wallenius.ppf(prob, M, n, N, odds))
True

產生隨機數字

>>> r = nchypergeom_wallenius.rvs(M, n, N, odds, size=1000)

方法

rvs(M, n, N, odds, loc=0, size=1, random_state=None)	隨機變數。
pmf(k, M, n, N, odds, loc=0)	機率質量函數。
logpmf(k, M, n, N, odds, loc=0)	機率質量函數的對數。
cdf(k, M, n, N, odds, loc=0)	累積分佈函數。
logcdf(k, M, n, N, odds, loc=0)	累積分佈函數的對數。
sf(k, M, n, N, odds, loc=0)	存活函數（也定義為 `1 - cdf` ，但 sf 有時更準確）。
logsf(k, M, n, N, odds, loc=0)	存活函數的對數。
ppf(q, M, n, N, odds, loc=0)	百分點函數（ `cdf` 的反函數 — 百分位數）。
isf(q, M, n, N, odds, loc=0)	反存活函數（ `sf` 的反函數）。
stats(M, n, N, odds, loc=0, moments=’mv’)	平均值（'m'）、變異數（'v'）、偏度（'s'）和/或峰度（'k'）。
entropy(M, n, N, odds, loc=0)	RV 的（微分）熵。
expect(func, args=(M, n, N, odds), loc=0, lb=None, ub=None, conditional=False)	函數（一個參數）相對於分佈的期望值。
median(M, n, N, odds, loc=0)	分佈的中位數。
mean(M, n, N, odds, loc=0)	分佈的平均值。
var(M, n, N, odds, loc=0)	分佈的變異數。
std(M, n, N, odds, loc=0)	分佈的標準差。
interval(confidence, M, n, N, odds, loc=0)	在 median 周圍具有相等面積的信賴區間。