scipy.interpolate.

make_lsq_spline

scipy.interpolate.make_lsq_spline(x, y, t, k=3, w=None, axis=0, check_finite=True, *, method='qr')

計算基於 LSQ（最小平方法）擬合 B 樣條的（係數）。

結果是線性組合

\[S(x) = \sum_j c_j B_j(x; t)\]

的 B 樣條基底元素，\(B_j(x; t)\)，它會最小化

\[\sum_{j} \left( w_j \times (S(x_j) - y_j) \right)^2\]

參數:

x陣列型, 形狀 (m,)

橫座標。

y陣列型, 形狀 (m, …)

縱座標。

t陣列型, 形狀 (n + k + 1,)。

節點。節點和資料點必須滿足 Schoenberg-Whitney 條件。

k整數, 選項性

B 樣條次數。預設為三次, k = 3。

w陣列型, 形狀 (m,), 選項性

樣條擬合的權重。必須為正數。如果為 None，則權重都相等。預設為 None。

axis整數, 選項性

插值軸。預設為零。

check_finite布林值, 選項性

是否檢查輸入陣列是否僅包含有限數字。停用可能會提高效能，但如果輸入包含無限大或 NaN，可能會導致問題（崩潰、無法終止）。預設為 True。

method字串, 選項性

解決線性 LSQ 問題的方法。允許的值為 “norm-eq”（顯式建構並求解法線方程組）和 “qr”（使用設計矩陣的 QR 分解）。預設為 “qr”。

回傳值:

b一個次數為 k 且節點為 t 的 BSpline 物件。

另請參閱

BSpline

表示 B 樣條物件的基底類別

make_interp_spline

用於插值樣條的類似工廠函數

LSQUnivariateSpline

基於 FITPACK 的樣條擬合常式

splrep

基於 FITPACK 的擬合常式

註解

資料點的數量必須大於樣條次數 k。

節點 t 必須滿足 Schoenberg-Whitney 條件，即必須有資料點 x[j] 的子集，使得 t[j] < x[j] < t[j+k+1]，對於 j=0, 1,...,n-k-2。

範例

在您的瀏覽器中試試看！

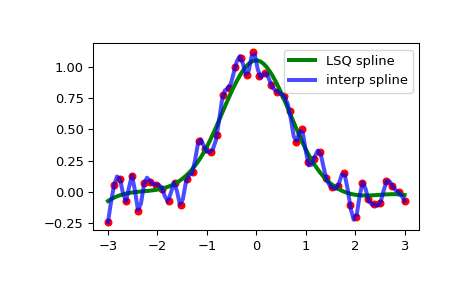
產生一些雜訊資料

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)

現在使用預定義的內部節點擬合平滑三次樣條。這裡我們通過添加邊界節點使節點向量 (k+1)-規則化

>>> from scipy.interpolate import make_lsq_spline, BSpline
>>> t = [-1, 0, 1]
>>> k = 3
>>> t = np.r_[(x[0],)*(k+1),
...           t,
...           (x[-1],)*(k+1)]
>>> spl = make_lsq_spline(x, y, t, k)

為了比較，我們也為同一組資料建構一個插值樣條

>>> from scipy.interpolate import make_interp_spline
>>> spl_i = make_interp_spline(x, y)

繪製兩者

>>> xs = np.linspace(-3, 3, 100)
>>> plt.plot(x, y, 'ro', ms=5)
>>> plt.plot(xs, spl(xs), 'g-', lw=3, label='LSQ spline')
>>> plt.plot(xs, spl_i(xs), 'b-', lw=3, alpha=0.7, label='interp spline')
>>> plt.legend(loc='best')
>>> plt.show()

NaN 處理：如果輸入陣列包含 nan 值，則結果無用，因為底層樣條擬合常式無法處理 nan。一種解決方法是對非數字資料點使用零權重

>>> y[8] = np.nan
>>> w = np.isnan(y)
>>> y[w] = 0.
>>> tck = make_lsq_spline(x, y, t, w=~w)

請注意需要用數值替換 nan（只要對應的權重為零，精確值並不重要。）

返回在新分頁中開啟