scipy.stats.Uniform.

plot#

Uniform.plot(x='x', y='pdf', *, t=('cdf', 0.0005, 0.9995), ax=None)[原始碼]#

繪製分布的函數圖。

用於快速視覺化隨機變數底層分布的便利函數。

參數:

x, ystr，可選: 字串，指示要用作橫座標和縱座標（水平和垂直座標）的量。預設值分別為 'x'（隨機變數的域）和 'pdf'（機率密度函數）。有效值為：‘x’、‘pdf’、‘cdf’、‘ccdf’、‘icdf’、‘iccdf’、‘logpdf’、‘logcdf’、‘logccdf’、‘ilogcdf’、‘ilogccdf’。
t3 元組，(str, float, float)，可選: 元組，指示要繪製量的範圍限制。預設值為 ('cdf', 0.001, 0.999)，表示將顯示分布的中心 99.9%。有效值為：‘x’、‘cdf’、‘ccdf’、‘icdf’、‘iccdf’、‘logcdf’、‘logccdf’、‘ilogcdf’、‘ilogccdf’。
axmatplotlib.axes，可選: 要在其上產生繪圖的軸。如果未提供，則使用目前軸。

回傳:

範例

使用所需的參數實例化分布

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> X = stats.Normal(mu=1., sigma=2.)

繪製分布中心 99.9% 範圍內的 PDF。與隨機樣本的直方圖進行比較。

>>> ax = X.plot()
>>> sample = X.sample(10000)
>>> ax.hist(sample, density=True, bins=50, alpha=0.5)
>>> plt.show()

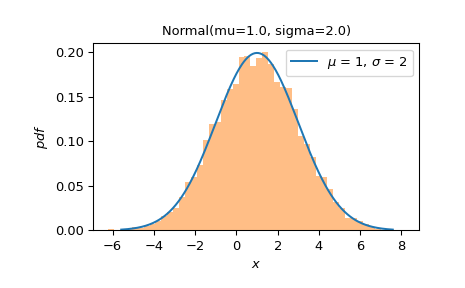
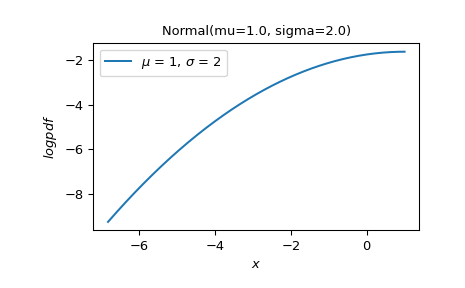
在左尾繪製 logpdf(x) 作為 x 的函數，其中 CDF 的對數介於 -10 和 np.log(0.5) 之間。

>>> X.plot('x', 'logpdf', t=('logcdf', -10, np.log(0.5)))
>>> plt.show()

繪製常態分布的 PDF 作為不同尺度參數值的 CDF 函數。

>>> X = stats.Normal(mu=0., sigma=[0.5, 1., 2])
>>> X.plot('cdf', 'pdf')
>>> plt.show()